MATH 548 - 001 - Spring 2022

MATH 548 - 001 - Spring 2022

Assignment 1

Due Tuesday, January 25, 2022

This first assignment is unusual. The goal here is to make sure you know how to use the SageMath software. The difficulty here should be technological, not mathematical. If you have any questions about this assignment, please contact the instructor early!

Problem 1

Find both an exact simplification and a decimal approximation for \(\sqrt{395317573779084}\).

Solution

The following code in SageMath:

x=sqrt(395317573779084)
print(x)
print(RR(x))

produces \(82346\sqrt{58299}\) and \(19882594.7446274\ldots\)

Problem 2

Consider the following integers: \[\begin{eqnarray} a&=&8866128975287528\\ b&=&8778405442862239\\ c&=&2736111468807040 \end{eqnarray}\] Compute \(a^3\), \(b^3+c^3\) and \(a^3-b^3-c^3\) exactly.

Solution

The following code in SageMath:

a = 8866128975287528
b = 8778405442862239
c = 2736111468807040
print(a^3)
print(b^3+c^3)
print(a^3-b^3-c^3)

show us that: \[\begin{eqnarray} a^3&=&696950821015779435648178972565490929714876221952\\ b^3+c^3&=&696950821015779435648178972565490929714876221919\\ a^3-b^3-c^3&=&33 \end{eqnarray}\]

Problem 3

Find an expanded exact expression for the complex number \(\frac{3+15i}{(24-7i)^2}\).

Solution

The following code in SageMath:

a=8866128975287528^3
b= 8778405442862239^3+2736111468807040^3
print(a)
print(b)
print(a-b)

produces the answer: \[\frac{3+15i}{(24-7i)^2} = - \frac{3459}{390625} + \frac{8913}{390625} i \].

Problem 4

Find all complex roots of the polynomial \(x^6 - 2x^5 + 27x^4 - 230x^3 + 414x^2 + 5632x + 7208\).

Solution

The following code in SageMath:

R.<x> = PolynomialRing(QQ)
f = x^6 - 2*x^5 + 27*x^4 - 230*x^3 + 414*x^2 + 5632*x + 7208
print(f.roots(CC))

tells us that there are 5 distincts roots: \(-2\), \(-2\pm 7i\), \(5 \pm 3i\).

Problem 5

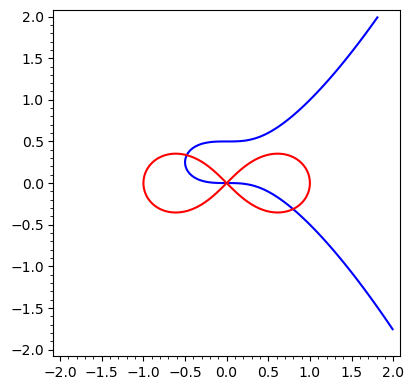
On the same axes, plot the curve satisfying \[x^3-2y^2+y=0\] and the curve satisfying \[(x^2+y^2)^2-(x^2-y^2)=0\] for \(x \in (-2,2)\) and \(y \in (-2,2)\).

Solution

Use the following SageMath code:

var("x,y")

plot1=implicit_plot(x^3-2*y^2+y, (x,-2,2), (y,-2,2), color="blue")
plot2=implicit_plot((x^2+y^2)^2-(x^2-y^2), (x,-2,2), (y,-2,2), color="red")
(plot1+plot2).show()

The result is as follows:

Problem 6

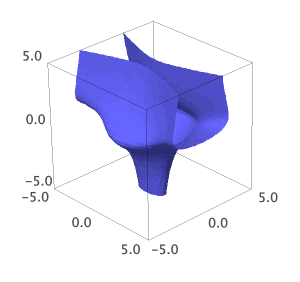
Plot the surface defined by \(x^2 + y^2-x^2 z + y^2 z^2=10\) for \((x,y,z)\) in the cube \([-5,5]^3 \subset \mathbb{R}^3\).

Solution

Use the following SageMath code:

var("x,y,z")

implicit_plot3d(x^2+y^2-x^2*z+y^2*z^2-10, (x,-5,5), (y,-5,5), (z,-5,5))

The result looks as follows: